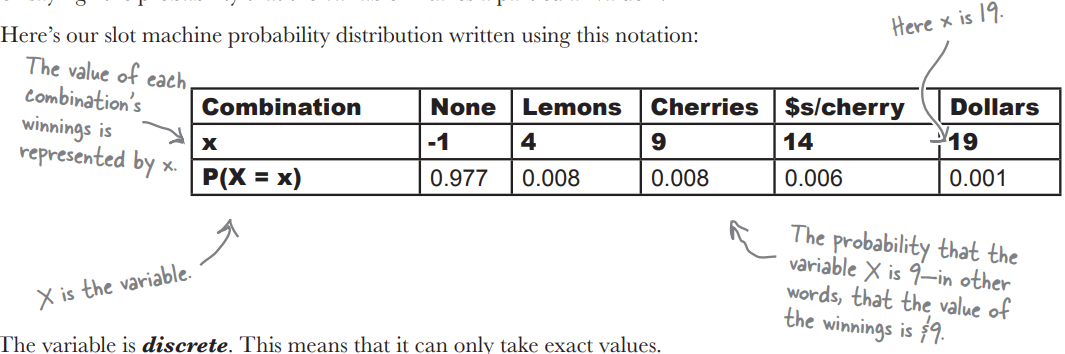
Discrete Probability Distributions

Discrete Probability Distribution

a type of probability distribution that shows all possible values of a discrete random variable along with the associated probabilities
Example:
probability distribution example.png|center

Expectation

E (X) = \sum x P (X = x)

Variance

V a r (X) = E (X - μ)^{2}

E (X - μ)^{2} = \sum (x - μ)^{2} P (X = x)

Standard Deviation

σ = \sqrt{V a r (X)}

Independent Observation

E (X_{1} + X_{2} + . . . X_{n}) = n E (X)

V a r (X_{1} + X_{2} + . . . X_{n}) = n V a r (X)

If you have independent variables $X$ and $Y$ then:

E (X + Y) = E (X) + E (Y)

E (X - Y) = E (X) - E (Y)

V a r (X + Y) = V a r (X) + V a r (Y)

V a r (X - Y) = V a r (X) + V a r (Y)

Linear Transforms

If you have a variable $X$ and numbers $a$ and $b$ then:

E (a X + b) = a E (X) + b

V a r (a X + b) = a^{2} V a r (X)

If you have a variable $X$ and variable $Y$ and numbers $a$ and $b$ then:

E (a X + b Y) = a E (X) + b E (Y)

E (a X - b Y) = a E (X) - b E (Y)

V a r (a X + b Y) = a^{2} V a r (X) + b^{2} V a r (Y)

V a r (a X - b Y) = a^{2} V a r (X) + b^{2} V a r (Y)

Sources: 1