Correlation and Regression

Definitions

Bivariate data

If one of the variables has been controlled in some way or is used to explain the other, it is called the independent or explanatory variable. The other variable is called the dependent or response variable.

Plot with a scatter diagram, one variable on the $x$ axis and the other on the $y$ axis

Correlation

Correlations are mathematical relationships between variables. It does not mean that one variable causes the other.

Linear Correlations

A linear correlation is one that follows a straight line.

Positive linear correlation is when low $x$ values correspond to low $y$ values, and high $x$ values correspond to high $y$ values.
Negative linear correlation is when low $x$ values correspond to high $y$ values, and high $x$ values correspond to low $y$ values.
If the values of $x$ and $y$ form a random pattern, then there’s no correlation.

Line of Best Fit

The line that best fits the data points is called the line of best fit.
Linear regression is a mathematical way of finding the line of best fit,

y = a + b x

The sum of squared errors, or SSE, is given by

\sum (y - \hat{y})^{2}

The slope of the line $y = a + b x$ is

b = \frac{\sum (x - \bar{x}) (y - \bar{y})}{\sum (x - \bar{x})^{2}}

The value of $a$ is given by

a = y - b x

The correlation coefficient, 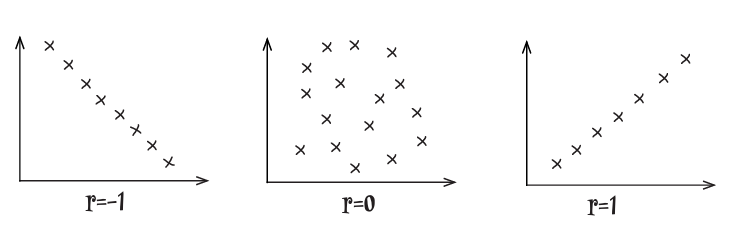$r$ , is a number between -1 and 1 that describes the scatter of data away from the line of best fit. If $r = - 1$ , there is perfect negative linear correlation. If $r = 1$ , there is perfect positive linear correlation. If $r = 0$ , there is no correlation. Correlation Coefficient.png|center
You find $r$ by calculating

r = \frac{b s_{x}}{s_{y}}

where

s_{x} = \sqrt{\frac{\sum (x - \bar{x})^{2}}{n - 1}}

and

s_{y} = \sqrt{\frac{\sum (y - \bar{y})^{2}}{n - 1}}

Least square regression alternate notation

covariance is $s_{x y}$ covariance of $x$ and $y$ is a measure of how $x$ and $y$ vary together

s_{x}^{2} = \frac{\sum (x - \bar{x})^{2}}{n - 1} s_{y}^{2} = \frac{\sum (y - \bar{y})^{2}}{n - 1} s_{x y} = \frac{\sum (x - \bar{x}) (y - \bar{y})}{n - 1}

b = \frac{s_{x y}}{s_{x}^{2}} r = \frac{s_{x y}}{s_{x} s_{y}}

the coefficient of determination

The coefficient of determination is given by $r^{2}$ or $R^{2}$ . It’s the percentage of variation in the $y$ variable that’s explainable by the $x$ variable.

r^{2} = (\frac{s_{x y}}{s_{x} s_{y}})^{2} o r r^{2} = \frac{\sum (y - \hat{y})^{2}}{\sum (y - \bar{y})^{2}}

non-linear relationships

If your line of best fit isn’t linear, you can sometimes transform it to a linear form.
You can then perform linear regression on the transformation to find the values of a and b. The big trick is to try and transform your non-linear equation of the line so that it takes the form

y^{'} = a + b x^{'}

where $y^{'}$ and $x^{'}$ are functions of $x$
Once you’ve transformed your y values, you can use least squares regression to find the values of $a$ and $b$ , then substitute these back into your original equation.

The confidence interval for the slope of a regression line

The confidence interval for b takes the form

\hat{b} \pm (m a r g i n o f e r r o r)

margin of error

m a r g i n o f e r r o r = t (ν) * (s t a n d a r d d e v i a t i o n o f b)

standard deviation of $b$

s_{b} = \frac{\sqrt{\frac{\sum (y - \hat{y})^{2}}{n - 2}}}{\sqrt{\sum (x - \bar{x})^{2}}}

confidence interval

(\hat{b} - t (ν) s_{b}, \hat{b} + t (ν) s_{b}) w h e r e ν = n - 2

Sources: 1